Sonic Geometry
artistic research by Nirantar Yakthumba
Nirantar Yakthumba is a musician and composer from Nepal, based in the Hague, the Netherlands. He is currently a Master’s student at the Institute of Sonology, with the help of a scholarship awarded to him by the Konrad Boehmer Foundation. In his research, he investigates the relations between sound, materials, force, and geometry, and how people individually and collectively make sense of these relations through practice.
During his Bachelor’s studies in composition at the Royal Conservatoire, the Hague, he studied composition with Peter Adriaansz, Calliope Tsoupaki, Cornelis de Bondt, and Jan van de Putte, as well as contemporary piano with Gerard Bouwhuis. He graduated with distinction in 2023.
research overview
In this research project, Niranthar investigates how a pink-noise signal can be constructed by chance based procedures in a timescale sensible to us and how this signal can be used to structure a musical practice.
छिन्नमस्ता (Chhinnamastā) is the productive outcome of this research, developed in collaboration
with members of the Kali Ensemble: Gregor Connelly, and Joel Gester Suárez. In this work, they articulate a highly precise method of listening and tuning that produces complex and ever changing periodic wave phenomena, distributing themselves in innumerable specific spatio temporal figures. Unlike a traditional fixed composition, Chhinnamastā is open in time and none of its moments are specified beforehand, only unfolding as three pink-noise signals are interpreted from the dice rolled by the players. As a result, the sounding waveforms gain a complexity that is immanent to the continuous perceptual process of the work — spread out over days, weeks, months, untempered durations — inscribed in any material that could document it.
noise/information?
In this research, Niranthar investigates the capacity for 1/f noise (pink noise) to inform a structural process occurring in real time. In this sense, pink noise constitutes a phenomenon that is wholly informative as opposed to one that obscures the process of decoding the ‘message’ of a signal. In other words, Niranthar does not presuppose any inherent distinction between noise and information.
What does it mean by noise and information? Drawing upon the noise-information-entropy paradigm of Claude Shannon and Cecile Malaspina’s interpretation of the applicability of this paradigm outside the regime of communications technology, I elaborate a suitable method for the development of my work Chhinnamastā.
In his seminal work A Mathematical Theory of Communication Shannon defines information as a measure of entropy, and in turn, entropy as a measure of freedom of choice. Let’s illustrate this formalism in the specific regime of text (deployed as a medium of communication). Then, the freedom of choice corresponds to choosing and ordering letters from a pre-determined alphabet. If the selection of each successive letter is completely uncorrelated to the sequence of selections that precede it, we are left with gibberish (noise). On the other hand, if the order of letters were completely unambiguous, the freedom of choice is null. The peculiarity of this instance is that because we know beforehand exactly what would follow each letter, new instantiations of the system repeat the same sequence of letters and hence are redundant and produce no information. It is clear how eliminating freedom of choice can only produce bare repetitions of a pre-determined signal.
However, in the middle of this spectrum of complexity (fully random, or fully determined), the succession of letters is still subject to a constraint (eg. a grammatical structure belonging to a particular linguistic practice), but by virtue of the ambiguity of possible selections for each grammatical state (two or more different letters may both fulfill the linguistic criteria to be selected), there is still a degree of freedom of choice. We can reasonably suppose that it is this structural regime where language can be said to operate, to the extent that language is open to processes of meaning production (one can choose what they say or write), while being subject to rules governing what is sensible to say. Taking a top-down approach, Shannon demonstrates how the English language, and hence its structure, can be approximated through a multi-level statistical analysis of various aspects of its structure, eg. the statistical frequency at which letters or words appear, the probability that a particular letter succeeds any determined sequence (of arbitrary length) of letters or words, etc.
In An Epistemology of Noise Malaspina speculates on the ramifications of Shannon’s theory of information-entropy in practices beyond communication. In particular, Malaspina demonstrates that in the narrow field of communication, the message — as the information to be transmitted
from a sender to a receiver — is already determined: ie. it is the task of communications engineers to develop techniques and technologies that perform the cut between what is desirable to transmit in a signal (the message) and what is undesirable to omit (noise). Shannon describes this problem or task in the following manner in the opening section of his text: “The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point.” (pp. 1).
Consequently, Malaspina raises the crucial question, how do we decide what is relevant and hence informative, versus what is irrelevant and hence obstructive, to processes of information outside the narrow regime of communication? To engage with this question entails a deep reconfiguration of our ideas of information and noise. Perhaps what we conventionally consider to be information is redundant and what we consider to be noise is unprecedented information that we are accustomed to ignore. Malaspina’s approach resonates with Barad’s agential realist
approach insofar as she postulates that, in general, there is no pre-determined message which must be revealed by reducing the noisy factors that obfuscate it; rather, information is produced only with the specification of an apparatus and a procedure of interpretation both of which come into practice through material-discursive experimentation.
Following this line of questioning, how can we think of tonal practices (practices of music that involve the production and organization of tones) in terms of Shannon’s information-entropy paradigm? At the very least, if we can recognize the uniqueness of different tonal practices, there must be processes that inform their individuation. How are decisions taken in the construction of musical instruments pertaining to particular practices? How do material-discursive conditions inform these decisions? How do instruments themselves determine material-discursive conditions for their use in musical practice?
Tuning systems are conventionally thought to be comprised of gamuts: ie. closed sets of related tones categorized as fixed modes, scales, temperaments, etc. If we take these closed gamuts as the set of symbols available to us as letters in an alphabet, then the composition of a tonal practice or language must consist of selecting tones from the gamut and ordering them according to specific techniques of tone composition. Some examples among countless others include the pakad and calan that structure North-Indian rāgas, the seyir that structure Turkish makam, and the rules of species counterpoint that structure European tonal harmony.
If we understand the selection of the gamut or tonal field as preceding the ordering of tones in time and the freedom of choice or information-entropy of a tonal practice presides largely in its tonal culture or its grammatical system: e.g. there may be multiple rāgas consisting of the same swara (tones), but they are uniquely identifiable according to their pakad (set of melodies that demonstrate the grammar of the rāga; Hindi: the act of grasping, holding, understanding; deriving from) and calan (how the rāga develops throughout its performance; Nepali: custom, practice, culture; Hindi: behaviour, fashion, usage, gait; from Sanskrit calati: to move, to turn). In this sense, the selection of specific gamuts constrains (whether that be due to practical reasons such as a limited number of keys or frets or other reasons) while the specific techniques of tonal composition informs (how the intended tonal phenomena are performed).
But what are the cultural origins of a gamut? In what soil inhere the conditions for their possibility? For example, as discussed in Chapter II, it seems as if western tonal harmony and its many components, like many musical infrastructures, just appeared into existence fully-formed. Analytical inquiry into the historical articulation of any musical (infra)structure immediately disposes of this first-order ignorance as to the nature of how musical cultures come to be, leaving us with higher-order ignorances (which we can understand as problems and questions for research) concerning the precise nature of the conditions that inform the decisions that produce the specificity of a cultural practice. Following Barad’s agential realism, to the extent that we
comprehend any cultural practice as apparatus-phenomenon, the adequacy and legitimacy of the notion and sense of a gamut is unfounded without the specification of the apparatus involved in its production. As a consequence, the idea that the gamut even precedes its ordering is questionable.
Chhinnamastā: Tonal Geometry
In his work, Niranthar problematizes the fixity of the gamut, in particular the 12-tone-equal-temperament system and its historical and cultural currency. For the past 5 years, he has been working on a heterogeneous set of formal, experimental, perceptual and micro-cultural methods of tonality that he calls the Dasamahavidya Tantra.
Chhinnamastā is a new addition to these methods that he began to work on in early 2024 with Paris-based ensemble ONCEIM. Niranthar continued developing this method with the help of his dear collaborators Joel Gester Suárez and Gregor Connelly—members of The Hague-based Kali Ensemble.
Work on Chhinnamastā began with a few speculations:
what kinds of tonalities would emerge if instead of selecting tones from a fixed ‘gamut’, we would instead select operations from a field of tonal relations?
what kind of (formal) strategies would we need to construct, tune, and practice in order to perform this continuous determination of the ‘gamut’ in performance?
what degree of certainty is possible to achieve for practitioners of this method? how does certainty determine the performance strategy?
From these initial speculations, Niranthar deduced that in order for the unfolding relations of this experimental gamut to be intelligible, the relation between the tones produced at each moment would have to be unambiguous. This meant that the piece would generate an operational (time) scale—independent of chronometric or rhythmic practices—depending only on the duration it takes for one to tune a tonal relation with certainty within an acceptable degree of accuracy and precision. As for the extending the notion of a fixed gamut of tones to a gamut of tonal relations, this would require instruments that are capable of free intonation. In the context of the western classical tradition, there are some instruments capable of this such as un-fretted string instruments, trombones, slide whistles, and various types of synthesizers, to name a few. Fretted instruments and instruments operated with keys, valves, fingering holes, and the likes are excluded due to the difficulty or impossibility to perform the music imagined according to the premise of this work.
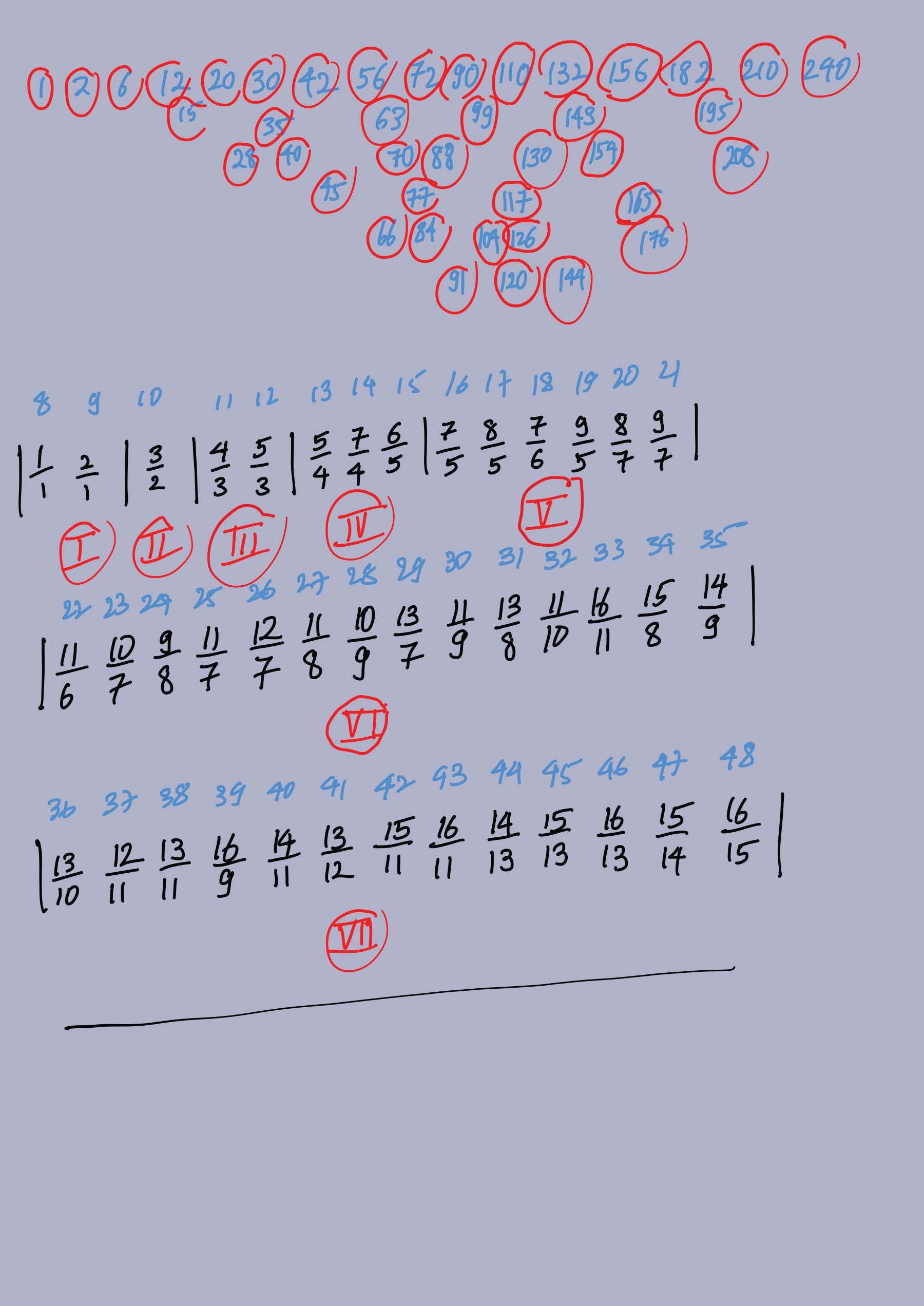
Because of the openness of this premise or speculative ground for the work, the idea to utilize pink-noise as a method to generate its structure came later rather than before the work was first conceived. To construct the pink-noise signal, I employ the algorithm outlined by mathematician Martin Gardner in Fractal Music, Hypercards, and More… (1991). Briefly, Gardner’s algorithm employs any number of random-number generators which are rolled sample-by-sample (the sample rate is arbitrary) in a specific order, let’s suppose we are using a regular six-sided dice:
the first dice is rolled on every sample and the number rolled (intensity) is recorded
the second dice is rolled every 2 samples and its intensity is recorded and stays fixed until the next time it is rolled
the third dice is rolled every 2x2 samples (4 samples) and similarly, its intensity is recorded and stays fixed until the next time it is rolled
the fourth dice is rolled every 2x2x2 samples (8 samples) and similarly, its intensity is recorded and stays fixed until the next time it is rolled, and so on…
generally, the n-th dice is rolled every 2x2x…x2 (n–1 times)—therefore, every 2n-1 samples— and its intensity is recorded and stays fixed until the next time it is rolled
at every sample, the intensities of all the dice are summed to a total intensity
For example, suppose we are operating at a sample-rate of 44.1 kHz, the 12th dice rolls every 211 samples (2048 samples, which is ~20 Hz). This procedure would produce a digital pink-noise signal in this specific sample-rate. Gardner explains that the pink-noise signal at any point exhibits fractal-structure because the dice rolled at longer sample rates contribute for longer periods of time, producing smooth variations in complexity. Gardner demonstrates how one can utilize this pink-noise algorithm as a control signal to structure melodies and rhythms from scales of notes or metric durations corresponding to pre-mapped intensities, eg. C4 = 1, C#4 = 2, … , B4 = 12, etc. In the article 1/f noise in music: Music from 1/f noise Richard F. Voss and John Clarke demonstrate how the spectral densities of conventional melodic structure—when analyzed as notes corresponding to a gamut of intensities—exhibits fractal structure conforming to the structures produced by pink-noise. Although, Voss and Clarke’s analyses are limited to particular musical cultures—namely, western classical, jazz and blues, and rock music—the structural correlation between pink-noise and the analysis of (aspects of) musical practice is fascinating, to say the least: the notion that even after enacting all sorts of cuts as to what constitutes appropriate musical material and what constitutes noise—eg. a desirable tone on a classical violin performance, or a particular rhythmic feeling, such as swing, in jazz—music can still exhibit characteristics of noise at the structural level.
This was enough motivation for me to build-in Gardner’s pink-noise algorithm into the method of my new work Chhinnamastā as a genuine experiment to experience what ramifications it would have in the development of its performance practice. While Gardner still implements the algorithm within the convention of pre-determined tones mapped onto a gamut and seeks to reproduce ‘conventional’ melodies and rhythms, I approach the algorithm from a experimental angle and explore its powerful implications in the case where tonal organization is produced by the procedure in performance rather than provided prior to performance.
This approach is a ramification of the complexity of opening-up tonality beyond its traditional modal expression, inspired by the questions asked by countless imaginative works in the field of artists engaged with tonality and intonation, namely: Daniil Pilchen, Lucie Nezri, Clara de Asís, Michael Winter, and Samuel Vriezen, many of whom are close collaborators and/or colleagues. In the same regard, I am also very grateful to have been exposed to the works of Eliane Radigue, Catherine Christer Hennix, James Tenney, Catherine Lamb, Chiyoko Szlavnics, Harry Partch, Ben Johnston, and Clarence Barlow, to name a few.
When experimenting on this method with ONCEIM, Niranthar worked-out various strategies to attempt this, which he refined with their help in workshops with the ensemble. Based on the instruments that were available in the ensemble, this version of the work was composed for trombonists Alexis Persigan, and Fabrice Charles, and Niranthar on electronics. Franz Hautzinger and Alan Regardin from ONCEIM took the roles of soothsayers in the piece, tasked with executing the pink-noise algorithm with dice and recording the results on paper. Lastly, Jean Daufresne played a fixed sub bass tone on the euphonium to provide a reference tone throughout the work. The result is an open-duration work where none of its moments are specified beforehand in a score but possesses a very articulate method.
Chhinnamastā: artistic research at studio LOOS
The second version of the work was developed at Studio LOOS and was made possible by the funding and support provided by the LOOS Foundation. The development of this work was motivated by the some of the challenges Niranthar faced in the first version of the work. The central challenge arose due to a problem relating to performance practice. To be specific, the method demanded much more time for practice than what was possible in the workshop scenario with ONCEIM. Related to this, several minor challenges arose from technical issues. While the trombonists played, Niranthar would process their signals through very narrow band-pass filters on SuperCollider to amplify specific harmonics. These harmonics would not always be audible or apparent to the trombonists. It was also a physically fatiguing method for the trombonists, who would have to sustain long tones while maintaining intensive and discerning attention on the harmonic fields they produced.
Niranthar approached these challenges by proposing the work to his close collaborators in the Kali Ensemble—Gregor Connelly and Joel Gester Suárez—adapting the work for synthesizers to shift the focus primarily to the aspects of tuning and developing techniques of perceptual precision. Each of them were equipped with 2 low-frequency harmonic oscillators, increasing the number of simultaneous oscillators (or crudely, instruments) from 2 to 6. Niranthar designed various types of synthesizers on SuperCollider based on subtractive synthesis techniques. The current version consists of sawtooth oscillators that are modulated with very low-gain pink-noise (SuperCollider UGen, not related to the dice procedure) passed through filter-banks consisting of the first 32 harmonics of the fundamental decreasing exponentially in amplitude. The filter-bank can additionally be shaped with a bell-curve equalizer and the rate of exponential decay of the amplitudes of the filter-bank frequencies is dependent on the signal amplitude (softer signals produce greater damping of higher partials while louder signals produce less). All parameters are controlled in real-time with midi-controllers, and the fundamental frequency of the oscillators are determined by 3 levels of fine tuning, the coarsest mapped from 30 Hz to 120, the first fine-tuning mapped between ±32 cents, and the second fine-tuning mapped between ±1 cent. The finest gradation of tuning in this case is 1/128 cent, meaning that the slowest beating that can be 1.35 × 10−4 produced with this apparatus is Hz (~7329 s, or roughly 2 hr 2 min 9 sec), corresponding to the difference between a frequency of 30 Hz and 30 Hz + 1/127 cent.
They had a total of 7 rehearsals of 3 hours each at Studio LOOS throughout May-June 2024. The extended amount of time that we were provided made it possible to explore the implications of this work as a social practice and activity of performing and listening together for long durations. The pink-noise structure makes itself known through these long durations, diverting in unprecedented ways every single sample. Every dice-roll produced a sound we had never heard before! And by virtue of the low-frequency oscillators that we were tuning, the way these tuned waveforms appeared in space were also unprecedented. In many senses, the method or system of Chhinnamastā is very much like a computer. but a bizarre one that performs calculations that diverge and converge, sometimes tangling and convoluting, and sometimes unraveling and simplifying. It is amusing to note that our sample-rate as a human-computer system averaged at roughly 15 minutes per sample! The strategy to perform this work was mostly an extension of the version for ONCEIM. Apart from the number of oscillators, the main differences are the following:
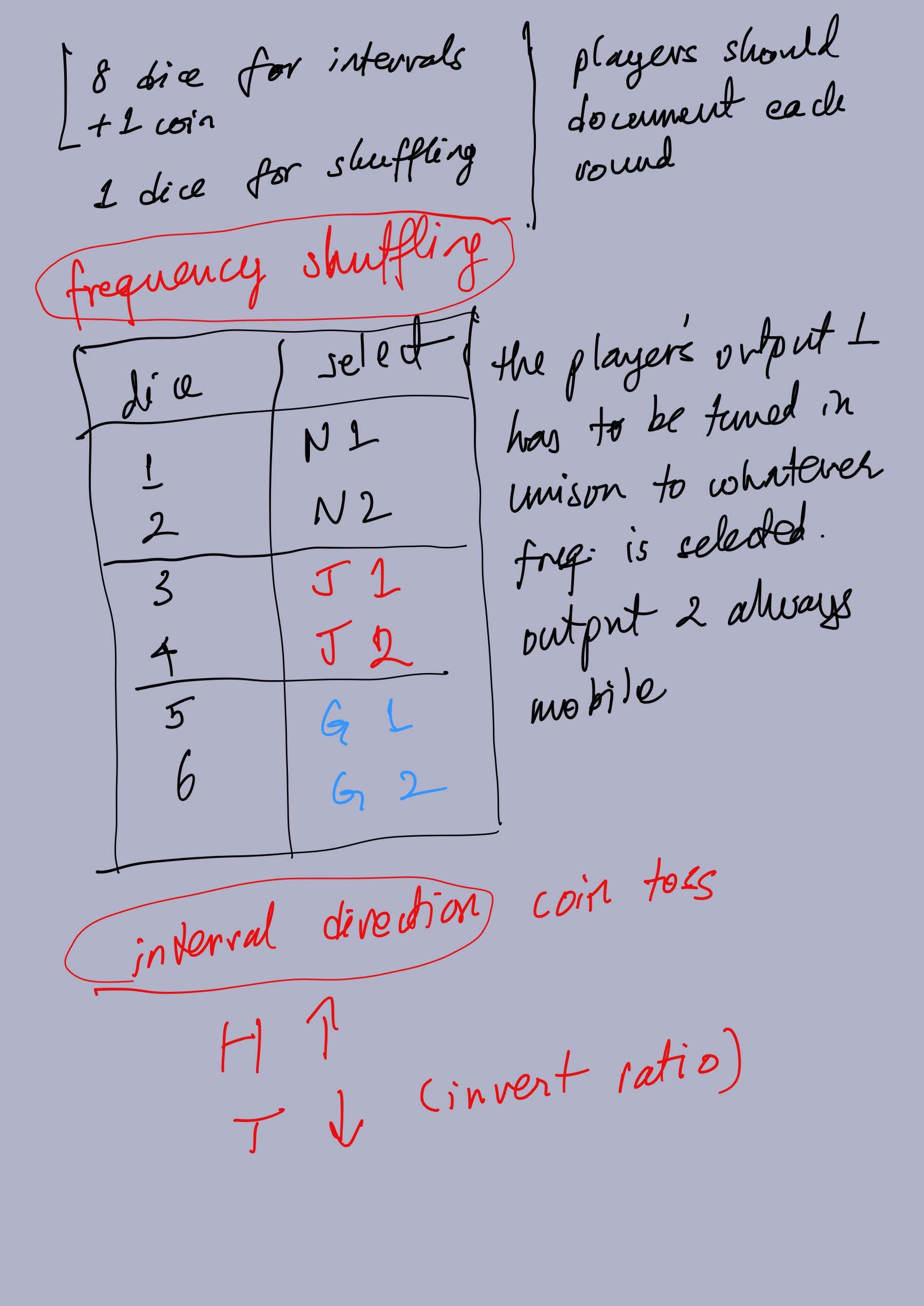
the intensities recorded on the dice were tabulated systematically for every sample
from the 2 oscillators that each musician operates, the first oscillator acts as the reference tone and stays fixed while the second oscillator is tuned relative to it
a coin is flipped for every sample to determine whether the interval is tuned higher or lower than the reference oscillator
a wider and more complex gamut of intervals is adopted and hence, more dice (8 instead of 3)
a procedure for ‘shuffling’ the 6 oscillators after tuning is implemented that correlates the 3 otherwise uncorrelated pink-noise dice algorithms; this produces sudden moments of simplicity, eg. when the first oscillators of all three musicians are tuned to the same tone
This research culminated in a recording of roughly 4 hours that stretches across these 7 rehearsals. The recording, as well as the updated gamut and the tabulations of the 16 samples performed and recorded at Studio LOOS are provided as additional documents along with this report. We also performed it as an abridged 15 minute presentation of the work in After Hours, at Museum Beelden aan Zee, on the 6th of September 2024.
To conclude, it is crucial to remark that the work is not fully archived or inscribed in any document, score, code, instrument, or recording but rather is embodied, memorized and produced in concreto in practice. Without the time and space where practitioners can experiment, learn, and negotiate the method, the work cannot be produced and remains in abstracto or speculative at best. It is in this sense that the entirety of the apparatus must be considered comprehensively as what constitutes the work itself and makes it possible. In the same sense, the phenomena that are produced by this apparatus are an expression of an intensive material-discursive network. Instruments are not just passive bodies waiting to be activated or sounded, rather, the entire set of agents and techniques participating in a process that not only makes possible but produces phenomena is what constitutes the truly instrumental.